Компьютерные тесты – мощный инструмент для оценки знаний учащихся, однако его использование требует аккуратности. К примеру, очень популярно использование тестов, состоящих из вопросов одиночного выбора. Предположим для простоты, что во всех этих вопросах есть три варианта ответа. Несложно показать, что учащийся, не желающий затруднять себя анализом вопросов и вариантов ответов, который решил положиться на судьбу и на все вопросы ответил наугад, в среднем наберет 33.3% возможных баллов. Если положительная оценка за тест может быть получена при меньшем количестве баллов, то любой учащийся, не обладающий знаниями, но умеющий считать, без труда получит положительную оценку.

Разумеется, приведенный выше случай является вырожденным, приведем другой более реальный. Предположим, что в тесте, состоящем из вопросов одиночного выбора с тремя вариантами ответов, проходной балл выставляется при правильном ответе на 2/3 вопросов.  Учащийся, знающий верные ответы только на 50% вопросов, легко задействует стратегию угадывания и, ответив на половину вопросов, в ответах на которые он уверен, не станет тратить время, а ответит на оставшиеся вопросы случайным образом. Очевидно, что в этом случае полученная им оценка (в среднем) составит 50% + 1/3*50% = 2/3, то есть именно то, что ему требовалось.

Из сказанного можно сделать простой вывод: составляя тест, необходимо учитывать возможность, что учащиеся применят стратегию угадывания, и принимать решение о шкале оценок с учетом этого фактора. Ниже приведены рекомендации на эту тему.

Для начала предложим два принципа, которые едва ли нуждаются в подробном обосновании:

1. Двое учащихся, одинаково ответивших на все вопросы теста, должны получить одинаковую оценку.
2. Учащийся, не знающий, как ответить ни на один вопрос, и применивший стратегию угадывания, должен получить нулевую оценку.

Следствием этих принципов является то, что нулевая оценка должна выставляться за количество баллов, меньшее или равное тому, которое в среднем получает учащийся, выбравший стратегию угадывания (то есть математическому ожиданию набранных баллов при этой стратегии). 

Рассмотрим четыре наиболее популярных типа вопроса и приведем некоторые рекомендации.

1. Контрольные вопросы одиночного выбора. Этот тип вопроса был уже рассмотрен выше. Вклад этого вопроса в математическое ожидание набранных баллов при задействовании стратегии угадывания , где h – оценка за вопрос, n – число вариантов ответа, а m – количество ответов, принимаемых как верные (использование параметра m, отличного от единицы – довольно редкая возможность, но, формально говоря, она также может быть использована).
2. Балльные вопросы одиночного выбора. Этот тип вопроса незначительно отличается от предыдущего. Его вклад в математическое ожидание  , где – оценка за вариант ответа, а n – число вариантов ответа.
3. Контрольные вопросы множественного выбора. Преимуществом этого типа вопроса является то, что вероятность угадывания верного ответа в нем существенно ниже, чем в вопросе одиночного выбора, разумеется, в том случае, если учащемуся не известно заранее, какое именно количество ответов – верные. В самом деле, при трех вариантах ответа вероятность угадать верный ответ равна 1/8, а при четырех – 1/16 (с той оговоркой, что как возможность отсутствия верных вариантов ответов, так и возможность того, что все ответы верные, не исключаются из рассмотрения). Однако этот тип вопроса имеет и существенный недостаток: в самом деле, в данном случае не предусмотрены «частично верные» ответы, любой ответ – либо верный (и тогда он вознаграждается предусмотренным количеством баллов), либо неверный (и тогда оценка за вопрос нулевая). Представим себе, что в вопросе десять вариантов ответа, и учащийся верно указал (то есть верно отметил как верные или верно не отметил как неверные) девять из них. В этом случае выставление нулевого количества баллов выглядит не вполне справедливо. Поэтому мы рекомендуем использовать этот тип вопроса при небольшом количестве вариантов ответа. 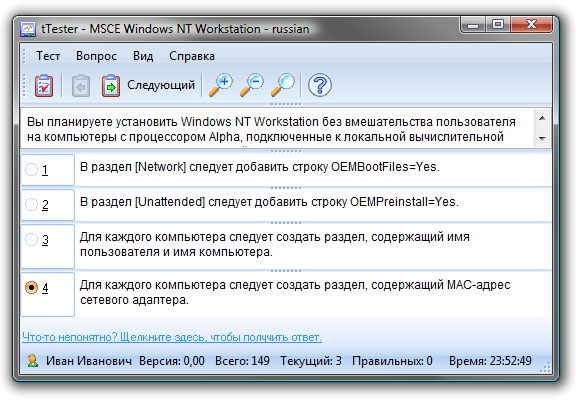Вклад этого вопроса в математическое ожидание , где h – оценка за вопрос, n – число вариантов ответа.
4. Балльные вопросы множественного выбора. Этот тип вопроса позволяет учитывать «частично верные» ответа, однако «не бесплатно». Приведем два важных замечания. 

• Во-первых, в отличие от балльных вопросов одиночного выбора, в балльном вопросе множественного выбора необходимо использовать отрицательные баллы, выставляемые за неверный вариант ответа, ошибочно отмеченный как верный. В самом деле, если не выставлять отрицательные баллы, то учащийся может просто отметить все варианты ответа как верные и, тем самым, получить максимально возможный балл. Следствие: при использовании вопросов этого типа учащийся может набрать отрицательное количество баллов, что может вызвать у него некоторое недоумение. Поэтому мы рекомендуем показывать учащемуся только оценку, не уточняя, какое количество баллов ей соответствует.
• Во-вторых, поскольку учащийся отмечает каждый вариант ответа как верный или не отмечает его как неверный независимо от того, как он отмечает иные варианты, то эти события независимы, и, следовательно, балльный вопрос множественного выбора с n вариантами ответа эквивалентен n контрольным вопросам одиночного выбора с двумя вариантами ответа. Иными словами, использование вопроса этого типа может сильно поднять планку «нулевой оценки». С учетом этого фактора данный тип вопроса показал себя как вполне эффективный.

Итак, вклад этого вопроса в математическое ожидани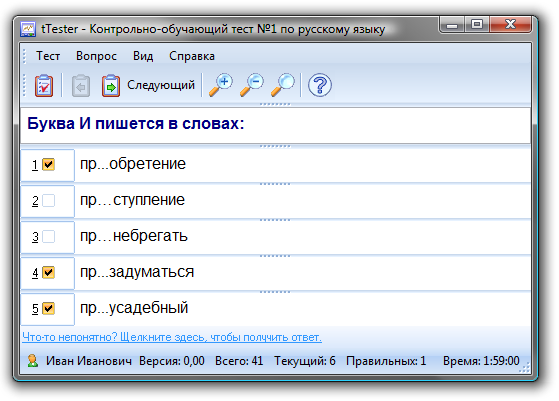е , где 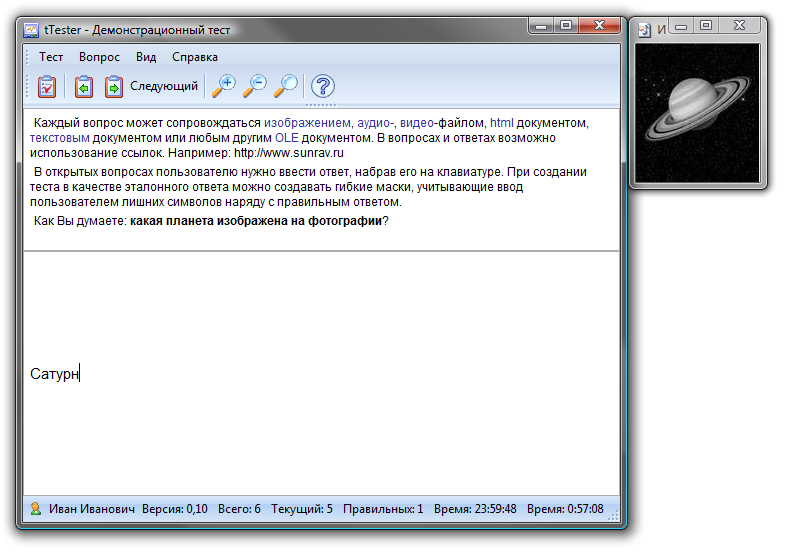– оценка за вариант ответа.

Резюмируем: при использовании вопросов одиночного и множественного выбора мы рекомендуем установить планку «нулевой оценки» (то есть количество баллов, за которое или за меньшее которого устанавливается нулевая оценка) на уровне , где N – число вопросов в тесте, а 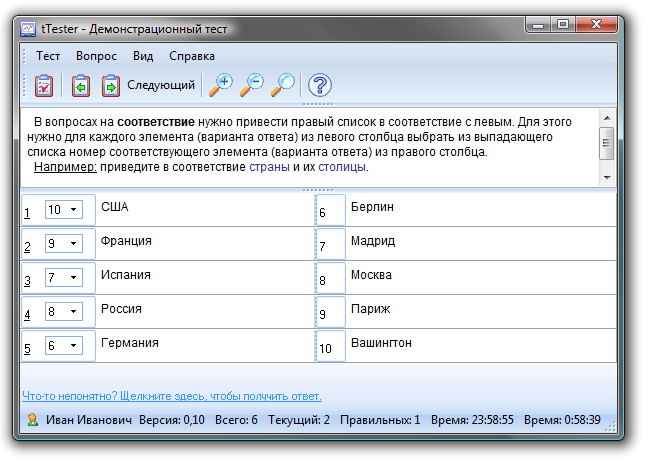вклад каждого вопроса, вычисляемый по приведенным выше формулам. Отрезок же от «нулевой планки» до максимального количества баллов может быть разделен на равные сегменты, соответствующие оценке, предъявляемой учащемуся.

Отметим, что в данном случае мы не включили в рассмотрение вопросы открытого типа, поля, выпадающие списки, а также вопросы соответствия и упорядочения списка. По нашему мнению, вероятность угадывания в этих случаях существенно ниже (за исключением выпадающего списка, эквивалентного контрольному вопросу одиночного выбора), чем в рассмотренных типах вопроса, или нулевая (в открытых вопросах или в полях). При необходимости же аналогичные вычисления могут быть легко проведены для вопросов соответствия и упорядочения списка.